HOMEWORK 04

Parallels between relative frequency and the axioms for probability

Andrey Kolmogorov was a Russian mathematician. In 1933, he contribuited to probability theory introducing his axioms: they are known today as probability theory fundamentals by the name of Kolmogorov axioms¹.

First Axiom

The probability of an event is a non-negative real number: \(P(E)\in\mathbb{R}, \quad P(E)\ge0 \quad \forall \ E\in F\)

where $F$ is the event space. It follows that $P(E)$ is always finite, in contrast with more general measure theory.

Second Axiom

This is the assumption of unit measure: that the probability that at least one of the elementary events in the entire sample space will occur is 1 \[P(Ω) = 1\]

Third Axiom

This is the assumpion of σ-additivity: Any countable sequence of disjoint sets $E_1, E_2,…$ satisfies \(P(\bigcup_{i=1}^{\infty}E_i)= \sum_{i=1}^{\infty} P(E_i)\)

We can find parallels of these axioms in relative frequency, let define $A$ and $B$ as events:

1. $0\leq f_A \leq 1$
2. $f(\emptyset)=0$ and $f(Population)=1$
3. $f_{A \cup B} = f_A + f_B - f_{A \cap B}$, where $f_{A \cap B} = 0$ if $A$ and $B$ are disjointed

These parallels could find explaantion in the so called “frequentist definition²” of probability, which claims that the probability of a random event denotes the relative frequency of occurrence of an experiment’s outcome when the experiment is repeated indefinitely. This interpretation considers probability to be the relative frequency “in the long run” of outcomes. (REMEMBER: multiple definition of probability were be given throughout the time)

Example of a Probability Measure Space

We indicate a probability space with a triplet (Ω, ε, P), where Ω is a sample space, ε is a σ-algebra of events and P is probability measure. (Explanation for this in the next section)

Think about tossing a coin:

$\Omega = \{ T, H \} $

$\epsilon = \{ \Omega, \emptyset , T, H, \bar{T}, \bar{H}, T \cup H, T \cap H \} $

Other examples:

• Positive integers: Ω = {1, 2, 3, . . . }

• Two tosses of a coin: Ω = {HH, HT , TH, T T}

Measure Theory as Foundation of Probability Theory

Probability Theory finds its foundation in Measure Theory³:

First let’s introduce the concept of σ-algebra⁴: in mathematical analysis and in probability theory, a σ-algebra on a set X is a nonempty collection Σ of subsets of X closed under complement, countable unions, and countable intersections.

Let now $X$ be a set and $\Sigma$ a $\sigma$ -algebra over $X$. A set function $\mu$ from $\Sigma$ to the extended real number line is called a measure if it satisfies the following properties:

Non-negativity: For all $E$ in $\Sigma$ , we have $\mu (E)\geq 0$.

Null empty set: $\mu (\varnothing )=0$.

Countable additivity (or $\sigma$ -additivity): For all countable collections $\{ E_{k}\}$ of pairwise disjoint sets in $\Sigma$,

If at least one set $E$ has finite measure, then the requirement that $\mu (\varnothing )=0$ is met automatically. Indeed, by countable additivity,

and therefore $\mu (\varnothing )=0$.

If the condition of non-negativity is omitted but the second and third of these conditions are met, and $\mu$ takes on at most one of the values $\pm \infty$ then $\mu$ is called a signed measure.

The pair $(X,\Sigma )$ is called a measurable space, and the members of $\Sigma$ are called measurable sets.

A triple $(X,\Sigma ,\mu )$ is called a measure space.

The requirements for a function $\mu$ to be a probability measure on a probability space are that:

• $\mu$ must return results in the unit interval [0,1] returning 0 for the empty set and 1 for the entire space

• Countable additivity

Application

The following application simulates m sequences of n trials distributed according a Binomial with success probability p and represent the following quantities: absolute frequency of success, relative frequency of success, “normalized” relative frequency of success. In the same chart, there’s a histogram representing the distribution of the above 3 types of frequencies on the last trial.

Download Link

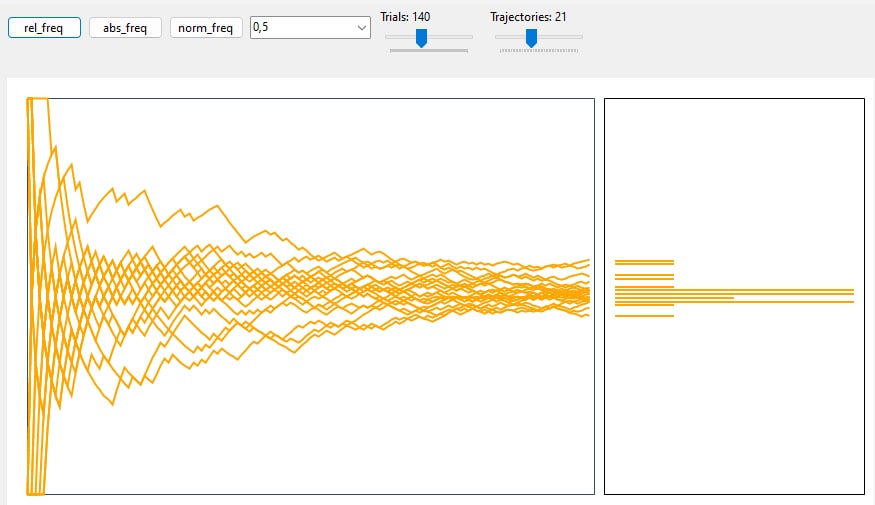
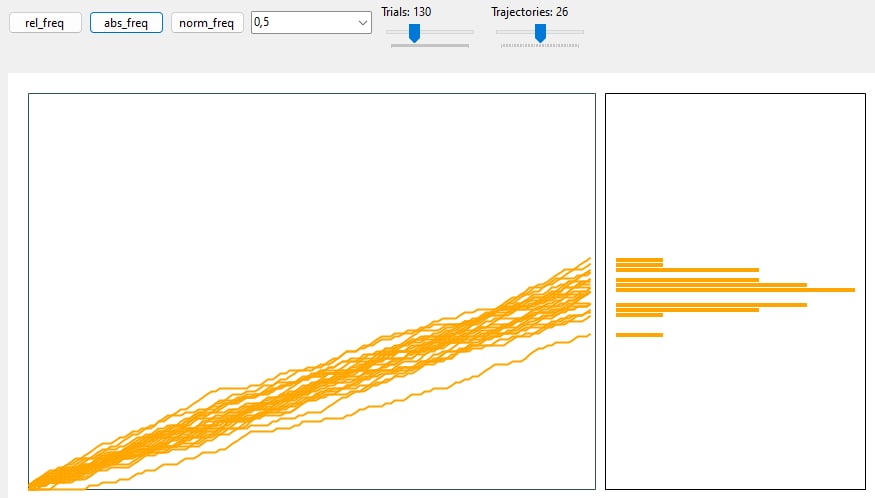
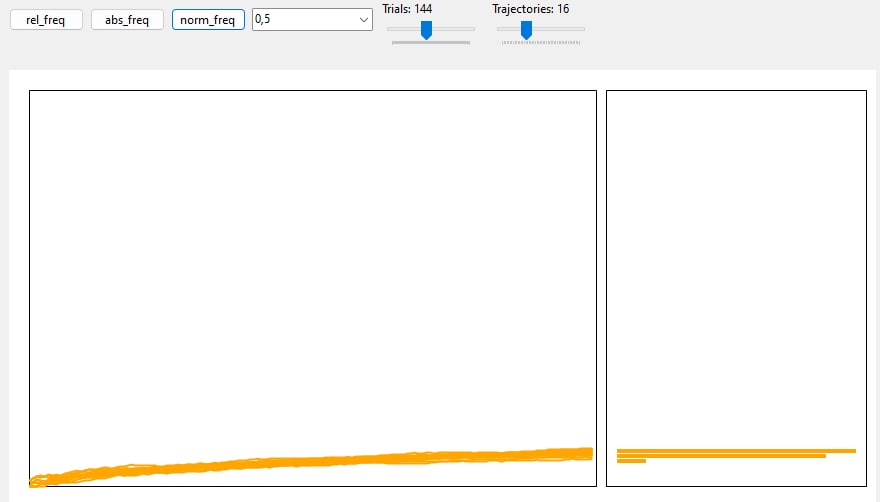
Code is also avaible on GitHub!

A simple introduction to graphics in the .NET environment. How to create a bitmap and a chart on it

To use graphics in the .NET environment we first declare a Bitmap object:

Bitmap bmp = new Bitmap(width, height);

This will be the image upon which we will be drawing. Then we have to declare a Graphics object which will be responsible of applying the low-level operations when drawing more complex shapes like lines and rectangles:

Graphics g = Graphics.FromImage(bmp);

To see the results of our actions, we will have to add the bitmap to a picture box by setting its Image property and by updating the picture box with the changes.

Once setup we can use many methods to plot charts on it, for example:

Pen pen = new Pen(Color.FromArgb(255, 255, 0, 0))
// line
g.DrawLine(pen, x1, y1, x2, y2);
//rectangle
g.DrawRectangle(pen, x, y, width, height);

How to get device coordinates from world coordinates

We can imagine that world coordinates live in a certain space, or interval. For every point in this interval, we want to migrate to other coordinates, made for our computer pixels. What we need is a linear transformation that change our points. By applying it to the world space we can reach the device space. These are the transformation for each variable

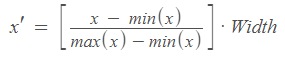
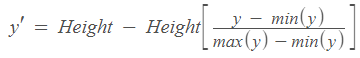
In C# we write them down like this:

        private double X_Normalization(double x, double w, double max, double min, int offset)
        {
            if ((max - min) == 0) return 0;
            return offset + w * (x - min) / (max - min);
        }

        private double Y_Normalization(double y, double h, double max, double min, int offset)
        {
            if ((max - min) == 0) return 0;
            return offset + h - h * (y - min)  / (max - min);
        }